U-value calculations are not the most interesting part of the design process. However, they are incredibly powerful tools that measure an incredibly important parameter of a building — energy efficiency. Given the fame of the word “sustainability” in the architectural scene nowadays, it pays to learn how to do such calculations. These allow you to design better wall assemblies, leading to more efficient cooling and heating, ultimately leading to less pollution and cost to the client. The benefits overpower the boredom of this topic. Let’s start at the beginning and work our way up.
What is U-value? Thermal transmittance and resistance explained
U-value is the technical term for the thermal transmittance of a single material or an assembly of materials, like walls and roofs. Put simply, it is a measure of how well a material insulates. The lower the U-value, the more the insulation. Lower U-values allow for much more efficient and cost-effective thermal comfort.
The unit of U-value is W/m2·°K. Let’s explain the unit through an example. Suppose the inside of a house clocks in at 300o Kelvin and the outside at 301o Kelvin. The U-value of the wall is 5 W/m2·°K. That means every square meter of wall area transfers 5 watts of heat from the outside to the inside. The unit can also be W/m²·°C, as per the convention, because Kelvin and Celsius are numerically equal, that is, a rise in temperature of 1°C is equal to a rise of 1°K.
Important to the concept of the U-value of a material is its thermal resistance. As the name suggests, thermal resistance is the measure of how much resistance a material offers to heat transfer through it. A great building envelope has a high thermal resistance and a low thermal transmittance, or U-value. Numerically, thermal resistance is the reciprocal of the U-value and its unit is m2·°K /W.
How to calculate the U-value of a material?
Let’s get down to the brass tacks. To calculate the U-value, first, we have to calculate the thermal resistance of each material in an assembly. The formula for the thermal resistance R of a material is
$$ R\; =\; \frac{d}{T} $$
In the above formula, d is the thickness of the material in meters and T is the thermal conductivity of the material. You can find a list of thermal conductivities of different building materials here.
Then, we have to calculate the total thermal resistance Rt of all the materials in the assembly. In addition to this, we also add the exterior and interior surface resistances, abbreviated as Rse and Rsi respectively. Surface resistance is the resistance offered by a thin film of air that is always present over the interior and exterior of a building element, like a wall. For India, default values of Rse and Rsi are approximately specified by the Bureau of Energy Efficiency as 0.05 m2·°K /W and 0.11 m2·°K /W respectively.
$$ R_t\ =\ R_{se} \ + \ R_{si}\ + \ R_1 \ + \ R_2 \ + \ R_3 \ …$$
In the above formula, R1, R2, and R3 are the thermal resistances of individual materials in an assembly.
After you calculate the total thermal resistance of a material, use this formula to calculate the U-value:
$$ U_{value}\;=\;\frac1{R_t}$$
Now that we know the methodology, let’s check out a real example.
Solved example
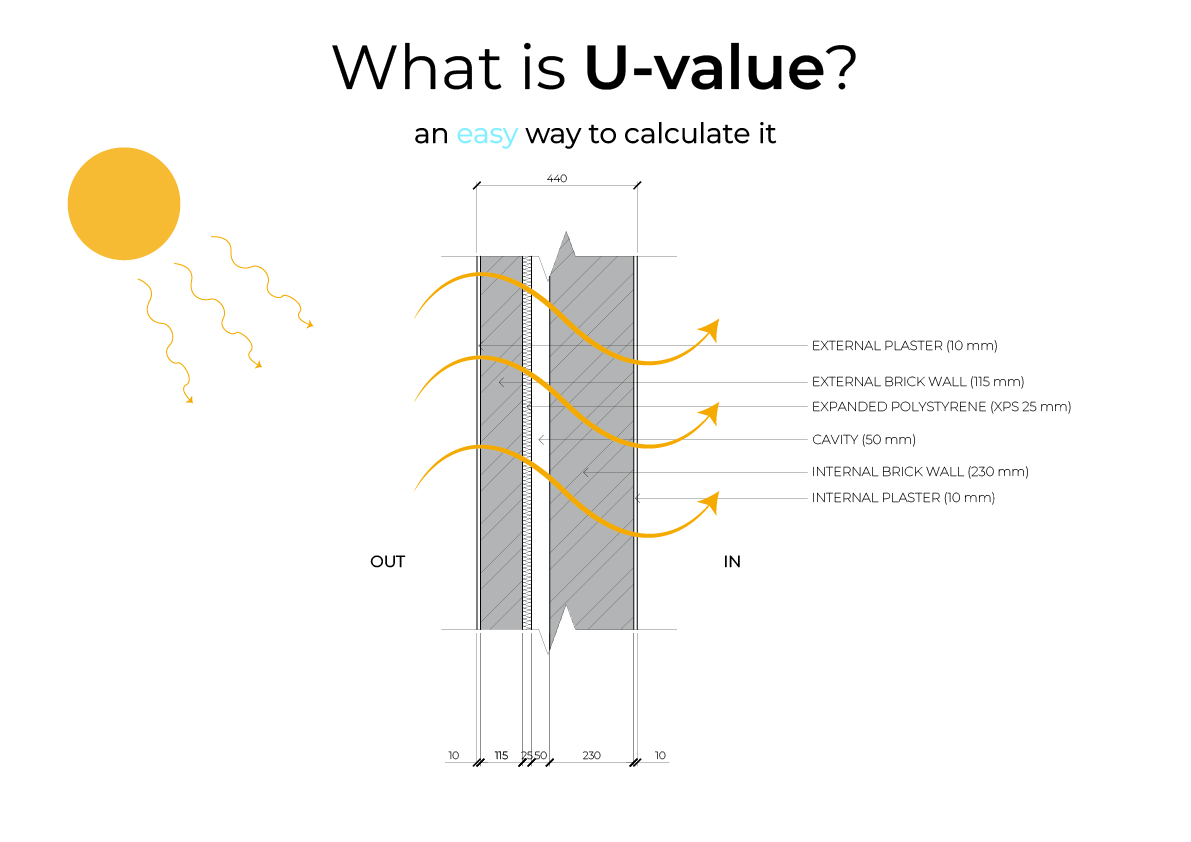
For this example, we will calculate the U-value of a simple cavity with a standard 115 mm thick brick wall on the exterior, followed by a 25 mm layer of expanded polystyrene (XPS), followed by a cavity of 50mm, and lastly, the interior brick wall of 230 mm. Cement plaster of 10 mm is on both sides of the wall. All the values of thermal conductivity have been taken from the Bureau of Energy Efficiency, India.

First, calculate all the individual resistances of the materials.
$$ R_{exterior\ wall}\ = \ \frac {0.115}{0.9} \ = \ 0.13 \ \ m^2·^oK /W \\ R_{interior\ wall}\ = \ \frac {0.230}{0.9} \ = \ 0.26\ \ m^2·^oK /W \\ R_{XPS}\ = \ \frac {0.025}{0.035} \ = \ 0.70\ \ m^2·^oK /W \\ R_{air \ cavity}\ = \ \frac {0.05}{2.84} \ = \ 0.02\ \ m^2·^oK /W \\ R_{internal\ plaster}\ = \ \frac {0.01}{0.721} \ = \ 0.01\ \ m^2·^oK /W \\ R_{external\ plaster}\ = \ \frac {0.01}{0.721} \ = \ 0.01\ \ m^2·^oK /W $$
Next, find the total thermal resistance of the wall assembly. Remember to add the external and internal surface resistances as well.
$$ R_{t}\ = \ 0.13\ + \ 0.26 \ + \ 0.7 \ + \ 0.02 \ + \ 0.01 \ + \ 0.01 \ + \ 0.05 \ + \ 0.11 \ \ m^2·^oK /W \\ = \ 1.29 \ \ m^2·^oK /W$$
Next, calculate the U-value.
$$ U_{value}\;=\;\frac1{1.29} \ \ W/m^2·^oK \\ = \ 0.78 \ \ W/m^2·^oK $$
And there is nothing more to it. If you practice calculating the U-value of simple wall or roof assemblies, you’ll get it into your head in no time. Of course, in reality, this value is not the final value because building envelopes are rarely uniform. Various thermal bridges and composite construction technologies complicate the process. These have to be accounted for in the calculation as well. However, the basic method remains the same.